はじめに
配管設計において、「曲がり部分の圧損（局所損失）」は無視できない要素です。特にエルボ（直角曲がり）やベンド（なだらかな曲がり）の使用数が多いシステムでは、圧損が全体の流量制限やポンプ選定に影響します。
この記事では、エルボやベンドの圧損の求め方、K値（損失係数）の使い方、よく使われる代表値を解説します。
ベンドとエルボの違い
曲管といえば、一般的にベンドとエルボが知られています。
その違いについて解説します。
ベンド（Bend）
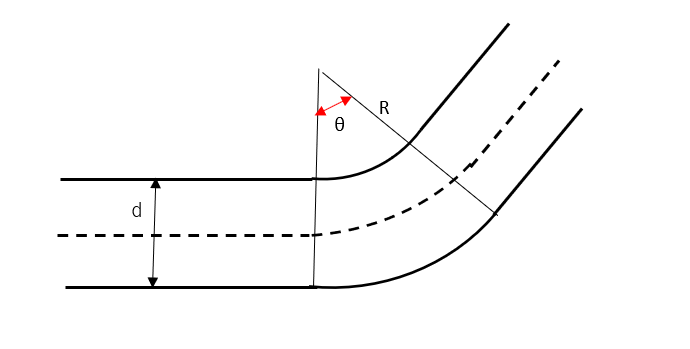
- 曲率半径が大きい
- 緩やかな曲がり
- 圧損が小さい傾向
エルボ（Elbow）
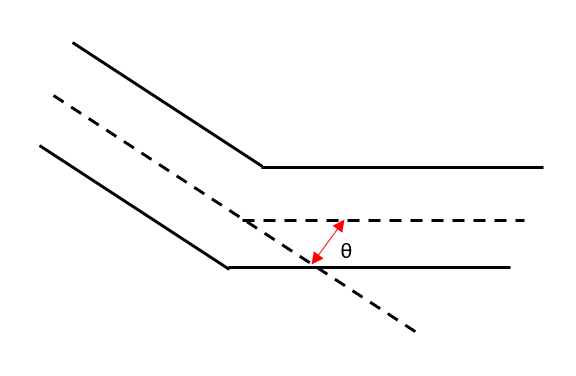
- 曲率が小さい
- 急な曲がり
- 圧損が大きい傾向
曲管の圧損はどう求める？
曲がり管は「局所損失」と呼ばれ、以下の式で圧損ΔPを求めるのが一般的です。
\( \Delta P = K \cdot \frac{1}{2} \rho V^2 \)
- \(\Delta P：圧力損失 [Pa]\)
- \(K：損失係数（形状・流れによる）\)
- \(\rho：流体の密度 [kg/m³]\)
- \(V：曲がり部の流速 [m/s]\)
ポイント
- この式は「全圧損」の一部を占める「局所損失」に対応しています。
- Kはエルボの角度・曲率半径・管径比・流速などで変わります。
K値の目安（90°エルボの場合）
| 曲がりの種類 | 標準K値（目安） |
|---|---|
| 90° エルボ | 約 0.75 |
| 90° エルボ | 約 0.3 |
| 長半径ベンド | 約 0.2 |
| 45° エルボ | 約 0.4 |
| スムーズなベンド | 約 0.1〜0.2 |
設計上の注意点
- ベンドを使うとK値が小さくなる → 圧損の低減になる
- ただし、スペースやコストの都合でエルボが選ばれることが多い
- エルボの数が多くなると、直管より局所損失の方が支配的になることもある
K値の計算に使用する計算式
ベンドでのK値予測式
\(K = 0.946 \cdot \left( \sin \frac{\theta}{2} \right)^2 + 2.05 \cdot \left( \sin \frac{\theta}{2} \right)^4\)
- \(\theta\)：曲がり角度 [度]
エルボでのK値予測式
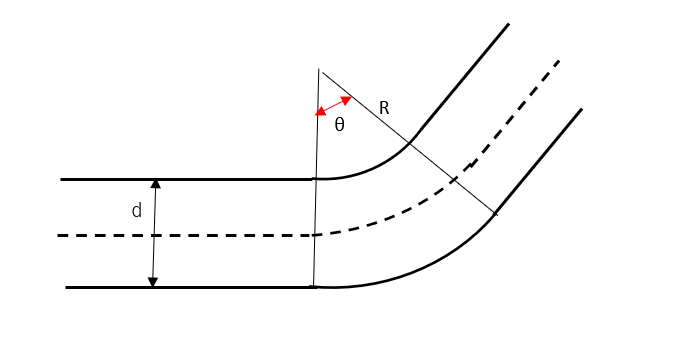
\(K = \left( 0.131 + 0.1632 \cdot \left( \frac{d}{R} \right)^{3.5} \right) \cdot \frac{\theta}{90}\)
- \(d：管の水力直径 [mm]（円形なら直径、長方形なら d= \frac{2WH}{W+H})\)
- \(R：曲率半径 [mm] \)
- \(\theta：曲がり角度 [度]\)
計算ツールの入出力
様々な流体種類、断面形状に対応して圧損を計算することができます。
🔧曲管の圧損計算ツール
ベンドとエルボで計算ツールを作成しました。ぜひご利用ください。
ベンド
エルボ
流体の密度・粘度一覧について
圧損計算を行う際には、流体の密度や粘度が重要なパラメータとなります。
本ツールでは代表的な流体を選択できるようにしていますが、より多くの流体や数値を確認したい場合は、下記の記事をご参照ください。
圧損計算と合わせて参照することで、実際の条件に近い値で計算でき、より正確な結果が得られます。
まとめ
- 曲がり管では、K値 × 1/2ρV²の式で圧損が計算される
- エルボよりベンドの方がK値が小さく、圧損は少ない
- 配管設計では、直管の摩擦損失と局所損失の合算が必要
- 実務では、K値一覧表を使って設計初期で概算すると効率的
おすすめ記事
様々な圧損の計算の仕方やツールについては、下記のリンクにてまとめています。
